This week, I asked my students to draft a “learning, teaching, and technology statement.” Their thoughts and insights pushed me to think more about my own beliefs. Although I have been exploring the relationships between learning, creativity, design, and teaching, I hadn’t ever articulated where “technology” fit in. (A bit ironic, seeing that I am an “assistant professor of learning design and TECHNOLOGY.”)
The great thing about teaching is that it’s not that different from learning–I’m sharing my ideas with others, which makes me clarify what those ideas are. And then I must connect those ideas with other content (currently, fitting my musings into the ISTE Standards for Educators), resulting in potentially cool combinations.
To start my “learning, teaching, and technology statement,” I reviewed some thoughts I shared on learning and creativity at several events last year (for example, see the first 4 minutes of this video). Basically, I use Kaufman and Beghetto’s 4-c creativity model to describe learning as personal meaning making (mini-c creativity). Learning then becomes seeing something differently in a useful way; forming a new understanding that is personally meaningful.
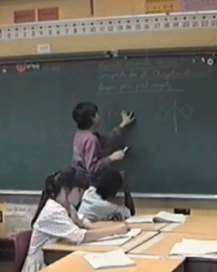
For example, consider Sean, a 3rd grade student in 1990 who was part of a University of Michigan research project (You can watch the video here). His class had been exploring even and odd numbers. Sean interrupted another discussion to say “I’ve been thinking about six.” He conjectured that six could be odd and even, because it can be made of 3 groups or 2 groups. Of course, Sean wasn’t using the standard definition of even and odd, but he had noticed something interesting: some even numbers are made up of an odd number of groups of 2. Interestingly, Euclid had also observed the same phenomenon. After much discussion, the class decides to call these special numbers “Sean’s Numbers.”
Sean’s idea about six is an example of mini-c creativity. The idea was personally meaningful and helped Sean make sense of a type of number. Through the process, the idea was explored, transformed, and combined with other students’ ideas.
This case demonstrates the close connection between creativity and learning. The teacher’s role was to design and facilitate this opportunity for learning, including establishing a classroom environment where students can engage in respectful critical discussions about their ideas. But what was the role of technology?
The central technology seen in the video is a chalkboard. Sean and Mei use the chalkboard to think through their own ideas, collaboratively develop new ideas, and communicate their ideas with others.
This got me thinking–what might digital technologies bring to this conversation? How might they change the learning?
Here’s what I came up with:
- Sean and his class could use some sort of simulation to explore number properties at a larger scale. For example, they might use a simulator like this to visualize patterns of numbers and identify which fit certain properties. In this case, the technology–its ability to instantly illustrate complex patterns–could help them see something differently.
- Sean could create a website about his special numbers. This would require he communicate his ideas through a combination of text, image, and maybe even sound, animation, and video. The process of creating this website (and linking it to other websites) might help Sean connect his thinking with other concepts. He could share his ideas and get feedback from a larger community of mathematicians. This approach would help him develop (mathematical) multimodal literacy and collaborate with others at a larger scale.
- Sean could integrate his ideas about numbers with other content areas, such as programming, art, and music. He could riff off of the ideas and creations of others, creating new combinations of meaning. For example, he might connect with the Scratch Numberblocks Band Studio and create a band of his special numbers, like TenNumberblocks’s Numberblocks Band but Odd Numbers (Tens Version) and Roman-Reigns_x03’s Square Number Band. Such an activity would allow Sean to explore mathematical concepts through creation.

Ultimately, Sean would be engaging in the networked and integrated thinking critical to 21st century success. Digital tools could help him see things differently, create, communicate, and collaborate.
And so, my final (for now) statement on learning, teaching, and technology:
- Learning is making meaning and seeing things differently.
- Teachers design and facilitate opportunities for learners to make and communicate meaning.
- Technologies can enhance this process by offering new (or more efficient) ways to understand, create, share, communicate, and collaborate.
Pingback: Teaching, Learning, Technology + Social Justice – Capricious Connections